matematika

Persamaan Dasar

sin x = sin a                  
cos x = cos a
tan x = tan a
*k = bilangan bulat
Catatan:
Jika ada persamaan cos x = sin a, cot x = tan a, sec x = cosec a, dan sebaliknya, salah satu diubah menjadi (90 – a)°,
contoh: cos x = sin a → cos x = cos (90 – a)°
Contoh:

• Tentukan HP (Himpunan Penyelesaian) dari 2 cos x – √3 = 0 untuk 0 ≤ x ≤ 360°

• Tentukan HP dari tan (60 – ½ x)° = cot (x + 120)° untuk 0 ≤ x ≤ 360°

Persamaan bentuk a cos nx + b sin nx

a cos nx + b sin nx diubah menjadi k cos(nx – α)
dimana
Selanjutnya diselesaikan seperti menyelesaikan persamaan dasar cos x = cos a
Penentuan letak α:

• Jika a +, b + → α di kuadran I
• Jika a –, b + → α di kuadran II
• Jika a –, b – → α di kuadran III
• Jika a +, b – → α di kuadran IV

Untuk persamaan a cos nx + b sin nx = c, syarat agar persamaan ini dapat diselesaikan:
Dan agar persamaan ini tidak dapat diselesaikan:

Persamaan bentuk a cos²x + b sin x.cos x + c sin²x = d

Caranya, lakukan dengan mengubah unsur-unsurnya seperti berikut ini:
Selanjutnya persamaan diselesaikan seperti menyelesaikan persamaan a cos nx + b sin nx = c

Persamaan bentuk a(cos x ± sin x) + b sin x.cos x + c = 0

Caranya:
Misalkan (cos x ± sin x) = p
maka
(cos x ± sin x)² = p²
cos²x ± 2 sin x.cos x + sin²x = p²
1 ± 2 sin x.cos x = p²
± 2 sin x.cos x = p² – 1
Sehingga 2 sin x.cos x = ± ½ (p² – 1)
Sehingga persamaan di atas akan menjadi persamaan kuadrat:
a.p ± ½ b(p² – 1) + c = 0
Selesaikan dengan cara pemfaktoran atau rumus abc untuk mendapatkan nilai p, kemudian persamaan cos x ± sin x = p dapat diselesaikan dengan cara seperti menyelesaikan persamaan a cos nx + b sin nx = c

Nilai ekstrim y = a cos nx + b sin nx + c

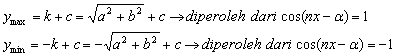
Pertidaksamaan Trigonometri

→ mencari harga nol sama dengan cara menyelesaikan persamaan trigonometri
→ diselesaikan dengan menggunakan garis bilangan
Contoh:
Selesaikan sin 2x < cos x  untuk 0 ≤ x ≤ 360°
Cara:
sin 2x – cos x < 0
2 sin x.cos x – cos x < 0
cos x.(2 sin x – 1) < 0
harga nol:

• cos x = 0

• 2 sin x – 1 = 0

Memberi tanda (+) dan (-) pada garis bilangan:
Jika x = 180° maka sin 2.180° – cos 180° = sin 360° – cos 180° = 0 – (–1) = 1 (+)
Jadi garis bilangannya:

karena yang diminta kurang dari (<) 0, maka yang diarsir adalah bagian-bagian yang bertanda (-)
Sehingga HP-nya: {0° ≤ x < 30° atau 90° < x < 150° atau 270° < x ≤ 360°}