|
Sifat akar-akar persamaan kuadrat
Jika x1 dan x2 adalah akar-akar persamaan kuadrat ax2 + bx + c = 0, maka:x1 + x2 = –b/a
x1.x2 = c/a
|x1 – x2| = –D/a
(Ingat! D = b2 – 4.a.c)
Bentuk simetri akar-akar persamaan kuadrat
Jumlah kuadrat akar-akar:x12 + x22 = (x1 + x2)2 – 2.x1.x2
Jumlah pangkat tiga akar-akar:
x13 + x23 = (x1 + x2)3 – 3.x1.x2.(x1 + x2)
Jumlah pangkat empat akar-akar:
x14 + x24 = (x12 + x22)2 – 2.x12.x22
Jumlah kebalikan akar-akar:
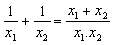
Jumlah kuadrat kebalikan akar-akar:
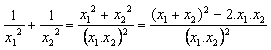
Selisih kuadrat akar-akar:
x12 – x22 = (x1 + x2).(x1 – x2) dimana x1 > x2
Hubungan Jenis Akar-akar PK dengan Nilai Diskriminan (D)
- Jika D > 0 maka PK mempunyai 2 akar real yang berlainan
→ D = bilangan kuadrat berarti akar-akarnya rasional
→ D bukan bilangan kuadrat berarti akar-akarnya irasional
- Jika D = 0 maka PK m,empunyai 1 akar real atau akar-akarnya kembar
- Jika D ≥ 0 maka PK mempunyai 2 akar real/nyata
- Jika D < 0 maka PK tidak mempuyai akar real / akar-akarnya imajiner
- Jika kedua akar positif (x1 > 0, x2 > 0)
D ≥ 0
x1 + x2 > 0
x1.x2 > 0
- Jika kedua akar negatif (x1 < 0 dan x2 < 0)
D ≥ 0
x1 + x2 < 0
x1.x2 > 0
- Jika kedua akar berlainan tanda (1 positif, 1 negatif)
D > 0
x1.x2 < 0
- Jika kedua akar bertanda sama (sama-sama positif/sama-sama negatif)
D ≥ 0
x1.x2 > 0
- Jika kedua akar saling berlawanan (x1 = –x2)
D > 0
b = 0 (diperoleh dari x1 + x2 = 0)
x1.x2 < 0
- Jika kedua akar saling berkebalikan (x1 = 1/x2)
D > 0
c = a
Contoh 1:Tentukan nilai m agar x2 + 4x + (m – 4) = 0 mempunyai 2 akar real
D ≥ 0
b2 – 4ac ≥ 0
42 – 4.1.(m – 4) ≥ 0
16 – 4m + 16 ≥ 0
–4m ≥ –16 – 16
Semua dibagi –4
(Ingat! Jika dibagi atau dikali bilangan negatif tanda pertidaksamaan dibalik)
m ≤ 4 + 4
m ≤ 8
Contoh 2:
Tentukan nilai n agar akar-akar PK x2 + (2n + 2)x + 5 – n = 0 bertanda sama
Syarat 1
D ≥ 0
b2 – 4ac ≥ 0
(2n + 2)2 – 4.1.(5 – n) ≥ 0
4n2 + 8n + 4 – 20 + 4n ≥ 0
4n2 + 12n – 16 ≥ 0
Semua dibagi 4:
n2 + 3n – 4 ³ 0
(n + 4).(n – 1) ³ 0
Pembuat nol: n = –4 atau n = 1
Syarat 2:
x1.x2 > 0

Gambar garis bilangan:

Jadi: HP = {n | n ≤ –4 atau 1 ≤ n < 5}
Menyusun PK
PK dengan akar-akar x1 dan x2 adalah:x2 – (x1 + x2)x + (x1.x2) = 0
dengan kata lain:x2 – (jumlah akar-akar)x + (hasil kali akar-akar) = 0
Contoh 1:Tentukan PK yang mempunyai akar-akar 2 dan –5:
x2 – (2 + (–5))x + (2.(–5)) = 0
x2 + 3x – 10 = 0
Contoh 2:
Jika x1 dan x2 adalah akar-akar PK: x2 – 3x – 1 = 0, susun PK baru yang akar-akarnya 3x1 + 2 dan 3x2 + 2!
Karena PK tersebut tidak dapat difaktorkan,
x1 + x2 = –b/a = –(– 3) /1 = 3
x1.x2 = c/a = –1/1 = –1
Misal akar-akar PK baru adalah y1 dan y2:
y1 + y2 = 3.x1 + 2 + 3.x2 + 2
= 3(x1 + x2) + 4 = 9 + 4 = 13
y1.y2 = (3x1 + 2).(3x2 + 2)
= 9.x1.x2 + 6.x1 + 6.x2 + 4
= 9.(–1) + 6.3 + 4 = –9 + 18 + 4 = 13
Jadi PK barunya:
x2 – (y1 + y2)x + (y1.y2) = 0
x2 – 13x + 13 = 0
Soal
Tentukan nilai k agar persamaan² kuadrat berikut memiliki akar kembar
a. x²-2x+k=0
b. 2x²-4x+k=0
c. kx²-6x+1/2=0
d. 3x²-kx+5=0
e. 2kx²+3x+2=0
a. x²-2x+k=0
b. 2x²-4x+k=0
c. kx²-6x+1/2=0
d. 3x²-kx+5=0
e. 2kx²+3x+2=0
Jawab
suatu persamaan kuadrat akan memiliki akar kembar jika D = 0
D = b² - 4ac
1.] x² - 2x + k = 0
D = 0
4 - 4 . 1 . k = 0
4 - 4k = 0
4k = 4
k = 1
2.] 2x² - 4x + k = 0
D = 0
16 - 4 . 2 . k = 0
16 - 8k = 0
8k = 16
k = 2
3.] kx² - 6x + 1/2 = 0
36 - 4 . k . 1/2 = 0
36 - 2k = 0
2k = 36
k = 18
4.] 3x² - kx + 5 = 0
D = 0
k² - 4 . 3 . 5 = 0
k² - 60 = 0
k = ± √60
5.] 2kx² + 3x + 2 = 0
D = 0
9 - 4 . 2k . 2 = 0
9 - 16k = 0
16k = 9
k = 9/16


masih binggung saya !!
Terima kasih atas informasinya!! ^^
Kalau x1^3x2 + x2^3x1 itu gimana ya? terimakasih~~
Klau akar akarnya tidak real?
terimakasih banyak, sangat membantu, keep posting...!
Terima kasih, sangat membantu
elamat sore kakak...saya pendatang baru mau minta tolong. kakak tolong bantuin saya mengerjakan tugas saya, ini soanya jika jika m dan n adalah akar-akar persamaan kuadrat x^2+5x+3=0 hitung nilai dari 1+m/1-m +1+n/1-n
elamat sore kakak...saya pendatang baru mau minta tolong. kakak tolong bantuin saya mengerjakan tugas saya, ini soanya jika jika m dan n adalah akar-akar persamaan kuadrat x^2+5x+3=0 hitung nilai dari 1+m/1-m +1+n/1-n
selamat sore kakak...saya pendatang baru mau minta tolong. kakak tolong bantuin saya mengerjakan tugas saya, ini soanya jika jika m dan n adalah akar-akar persamaan kuadrat x^2+5x+3=0 hitung nilai dari 1+m/1-m +1+n/1-n
OK mas brow. sukron kasiron
Bego lu
Lol wkwkwk selow m8
Kalau X1^2+X2^2-6X1X2 itu jadinya gimana?
makasih d butuhin bwt tes tpa...
terima kasih, sangat membantu.
Mksih banyak, informasinya mudah di tangkap...
����
Terimakasih, artikelnya sungguh sangat membantu saya dalam memahami materi sifat akar PK. :)
-4/9 mbak.
Msih idup kgk?
akmj
Bukannya x1-x2 = -akar D/a
Terima kasih, sgt membantu saya 😍
1+m/1-m+1+n/1-n
{(1-m+m)/1-m}+{(1-n-n)/1-n}
(1/1-m)+(1/1-n)
(1-n+1-m)/(1-m)(1-n)
{2-(n+m)}/1-(m+n)+mn
so, dari x^+5x+3=0 didapat m+n=-5 dan mn=3
subtitusi menjadi {2-(-5)}/{1-(-5)+3}=7/9
bukan kak , berdasarkan teori memang x1-x2=( akar D)/a
Kalau
(X1+3)+(x2+3) gimana?
Asiyap
MAKASIH Y KAK