matematika

Ukuran Sudut

1 putaran = 360 derajat (360°) = 2π radian

Perbandingan trigonometri

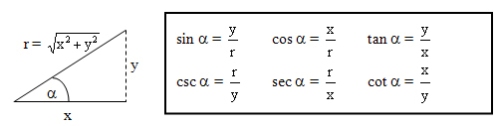
Catatan:

• Sin = sinus
• Cos = cosinus
• Tan/Tg = tangens
• Sec = secans
• Cosec/Csc = cosecans
• Cot/Ctg = cotangens

Dari gambar tersebut dapat diperoleh:

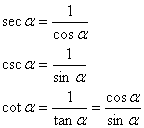
(sec merupakan kebalikan dari cos,
csc merupakan kebalikan dari sin, dan
cot merupakan kebalikan dari tan)
Contoh:
Dari segitiga berikut ini:

Diketahui panjang AB = 12 cm, AC = 13 cm. Hitung semua nilai perbandingan trigonometri untuk sudut A!
Pertama, hitung dulu panjang BC dengan menggunakan rumus Phytagoras:

Nilai perbandingan trigonometri beberapa sudut istimewa

* tambahan: sin 37° = cos 53° = 0,6

Kuadran

Kuadran adalah pembagian daerah pada sistem koordinat kartesius → dibagi dalam 4 daerah
Nilai perbandingan trigonometri untuk sudut-sudut di berbagai kuadran memenuhi aturan seperti pada gambar:

Untuk sudut b > 360° → b = (k . 360 + a) → b = a
(k = bilangan bulat > 0)
Mengubah fungsi trigonometri suatu sudut ke sudut lancip

• Jika menggunakan 90 ± a atau 270 ± a maka fungsi berubah:

• Jika menggunakan 180 ± a atau 360 ± a maka fungsi tetap

Sudut dengan nilai negatif
Nilai negatif diperoleh karena sudut dibuat dari sumbu x, diputar searah jarum jam
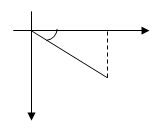Untuk sudut dengan nilai negatif, sama artinya dengan sudut yang berada di kuadran IV
Contoh:

• Cos 120º = cos (180 – 60)º = – cos 60º = – 1/2 (120º ada di kuadran II sehingga nilai cos-nya negatif)
• Cos 120º = cos (90 + 30)º = – sin 30º = – 1/2
• Tan 1305º = tan (3.360 + 225)º = tan 225º = tan (180 + 45)º = tan 45º = 1 (225º ada di kuadran III sehingga nilai tan-nya positif)
• Sin –315º = – sin 315º = – sin (360 – 45)º = –(– sin 45)º = sin 45º = 1/2 √2

Identitas Trigonometri

Grafik fungsi trigonometri

y = sin x

y = cos x

y = tan x

y = cot x

y = sec x

y = csc x

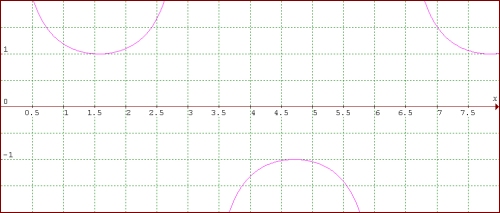
Menggambar Grafik fungsi y = A sin/cos/tan/cot/sec/csc (kx ± b) ± c

1. Periode fungsi untuk sin/cos/sec/csc = 2π/k → artinya: grafik akan berulang setiap kelipatan 2π/k

2. Nilai maksimum = c + |A|, nilai minimum = c – |A|
3. Amplitudo = ½ (y_max – y_min)
4. Cara menggambar:
1. Gambar grafik fungsi dasarnya seperti pada gambar di atas
2. Hitung periode fungsi, dan gambarkan grafik sesuai dengan periode fungsinya
3. Jika A ≠ 1, kalikan semua nilai y pada grafik fungsi dasar dengan A
4. Untuk kx + b → grafik digeser ke kiri sejauh b/k

5. Untuk + c → grafik digeser ke atas sejauh c

Contoh: y = 2 sin (3x + 90)° + 3
→ periode fungsi = 2p/3 = 120°
Langkah-Langkah:
Grafik fungsi y = sin x

Karena periode fungsinya 2π/3, maka dalam selang 0 hingga 2π, terjadi 3 gelombang sinus → y = sin 3x

Ampitudo dikali 2 → y = 2 sin 3x

Grafik digeser ke kiri sejauh 90°/3 = 30° = π/6 → y = 2 sin (3x + 90)°

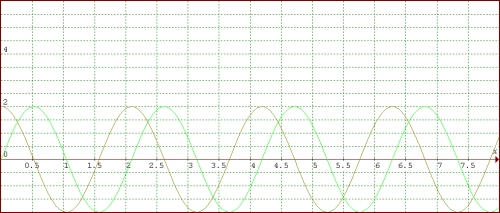
Grafik digeser ke atas sejauh 3 satuan → y = 2 sin (3x + 90)° + 3

Aturan-Aturan pada Segitiga ABC

Aturan Sinus
Dari segitiga ABC di atas:

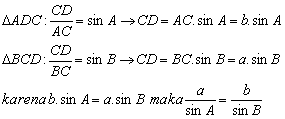
Sehingga, secara umum, dalam segitiga ABC berlaku rumus:

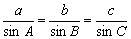
Aturan Cosinus
Dari segitiga ABC di atas:

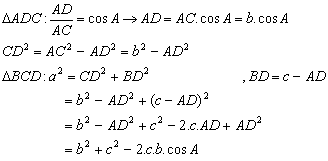
Sehingga, secara umum:

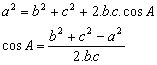
Luas Segitiga
Dari segitiga ABC di atas diperoleh:

Sehingga, secara umum:

Rumus Jumlah dan Selisih Sudut

Dari gambar segitiga ABC berikut:

AD = b.sin α
BD = a.sin β
CD = a.cos β = b.cos α

Untuk mencari cos(α+β) = sin (90 – (α+β))°


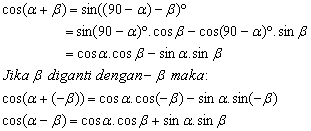
Untuk fungsi tangens:

Sehingga, rumus-rumus yang diperoleh adalah:

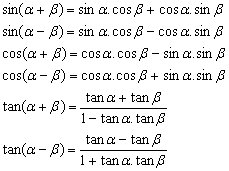
 Rumus Sudut Rangkap

Sehingga, rumus-rumus yang diperoleh adalah:
Penurunan dari rumus cos2α:

Rumus Perkalian Fungsi Sinus dan Kosinus

Dari rumus-rumus jumlah dan selisih dua sudut dapat diturunkan rumus-rumus baru sebagai berikut: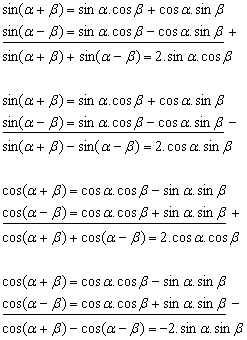

Sehingga, rumus-rumus yang diperoleh:

Rumus Jumlah dan Selisih Fungsi Sinus dan Kosinus

Dari rumus perkalian fungsi sinus dan kosinus dapat diturunkan rumus jumlah dan selisih fungsi sinus dan kosinus.

Maka akan diperoleh rumus-rumus:

Contoh-contoh soal:
(1) Tanpa menggunakan daftar, buktikan bahwa:


(2) Buktikan bahwa dalam segitiga ABC berlaku: