|
Sifat-Sifat Pertidaksamaan
- tanda pertidaksamaan tidak berubah jika kedua ruas ditambah atau dikurangi dengan bilangan yang sama
Jika a < b maka:
a + c < b + c
a – c < b – c
- tanda pertidaksamaan tidak berubah jika kedua ruas dikali atau dibagi dengan bilangan positif yang sama
Jika a < b, dan c adalah bilangan positif, maka:
a.c < b.c
a/b < b/c
- tanda pertidaksamaan akan berubah jika kedua ruas pertidaksamaan dikali atau dibagi dengan bilangan negatif yang sama
Jika a < b, dan c adalah bilangan negatif, maka:
a.c > b.c
a/c > b/c
- tanda pertidaksamaan tidak berubah jika kedua ruas positif masing-masing dikuadratkan
Jika a < b; a dan b sama-sama positif, maka: a2 < b2
Pertidaksamaan Linear
→ Variabelnya berpangkat 1Penyelesaian:
Suku-suku yang mengandung variabel dikumpulkan di ruas kiri, dan konstanta diletakkan di ruas kanan
Contoh:

Pertidaksamaan Kuadrat
→ Variabelnya berpangkat 2Penyelesaian:
- Ruas kanan dibuat menjadi nol
- Faktorkan
- Tentukan harga nol, yaitu nilai variabel yang menyebabkan nilai faktor sama dengan nol
- Gambar garis bilangannya
Jika tanda pertidaksamaan ≥ atau ≤, maka harga nol ditandai dengan titik hitam •
Jika tanda pertidaksamaan > atau <, maka harga nol ditandai dengan titik putih °
- Tentukan tanda (+) atau (–) pada masing-masing interval di garis bilangan. Caranya adalah dengan memasukkan salah satu bilangan pada interval tersebut pada persamaan di ruas kiri.
Tanda pada garis bilangan berselang-seling, kecuali jika ada batas rangkap (harga nol yang muncul 2 kali atau sebanyak bilangan genap untuk pertidaksamaan tingkat tinggi), batas rangkap tidak merubah tanda
- Tentukan himpunan penyelesaian
→ jika tanda pertidaksamaan > 0 berarti daerah pada garis bilangan yang diarsir adalah yang bertanda (+)
→ jika tanda pertidaksamaan < 0 berarti daerah pada garis bilangan yang diarsir adalah yang bertanda (–)
Contoh:(2x – 1)2 ≥ (5x – 3).(x – 1) – 7
4x2 – 4x + 1 ≥ 5x2 – 5x – 3x + 3 – 7
4x2 – 4x + 1 – 5x2 + 5x + 3x – 3 + 7 ≥ 0
–x2 + 4x + 5 ≥ 0
–(x2 – 4x – 5) ≥ 0
–(x – 5).(x + 1) ≥ 0
Harga nol: x – 5 = 0 atau x + 1 = 0
x = 5 atau x = –1
Garis bilangan:
- menggunakan titik hitam karena tanda pertidaksamaan ≥
- jika dimasukkan x = 0 hasilnya positif
- karena 0 berada di antara –1 dan 5, maka daerah tersebut bernilai positif, di kiri dan kanannya bernilai negatif
- karena tanda pertidaksamaan ≥ 0, maka yang diarsir adalah yang positif

Jadi penyelesaiannya: {x | –1 ≤ x ≤ 5}
Pertidaksamaan Tingkat Tinggi
→ Variabel berpangkat lebih dari 2Penyelesaian sama dengan pertidaksamaan kuadrat
Contoh:
(2x + 1)2.(x2 – 5x + 6) < 0
(2x + 1)2.(x – 2).(x – 3) < 0
Harga nol: 2x + 1 = 0 atau x – 2 = 0 atau x – 3 = 0
x = –1/2 atau x = 2 atau x = 3
Garis bilangan:
- menggunakan titik putih karena tanda pertidaksamaan <
- jika dimasukkan x = 0 hasilnya positif
- karena 0 berada di antara –1/2 dan 2, maka daerah tersebut bernilai positif
- karena –1/2 adalah batas rangkap (–1/2 muncul sebanyak 2 kali sebagai harga nol, jadi –1/2 merupakan batas rangkap), maka di sebelah kiri –1/2 juga bernilai positif
- selain daerah yang dibatasi oleh batas rangkap, tanda positif dan negatif berselang-seling
- karena tanda pertidaksamaan ³ 0, maka yang diarsir adalah yang positif

Jadi penyelesaiannya: {x | 2 < x < 3}
Pertidaksamaan Pecahan
→ ada pembilang dan penyebutPenyelesaian:
- Ruas kanan dijadikan nol
- Samakan penyebut di ruas kiri
- Faktorkan pembilang dan penyebut (jika bisa)
- Cari nilai-nilai variabel yang menyebabkan pembilang dan penyebutnya sama dengan nol (harga nol untuk pembilang dan penyebut)
- Gambar garis bilangan yang memuat semua nilai yang didapatkan pada langkah 4
Apapun tanda pertidaksamaannya, harga nol untuk penyebut selalu digambar dengan titik putih (penyebut suatu pecahan tidak boleh sama dengan 0 agar pecahan tersebut mempunyai nilai)
- Tentukan tanda (+) atau (–) pada masing-masing interval
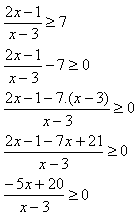
Harga nol pembilang: –5x + 20 = 0
–5x = –20 → x = 4
Harga nol penyebut: x – 3 = 0 → x = 3
Garis bilangan:
→ x = 3 digambar menggunakan titik putih karena merupakan harga nol untuk penyebut

Jadi penyelesaiannya: {x | 3 < x ≤ 4}
Contoh 2:

Harga nol pembilang: x – 2 = 0 atau x + 1 = 0
x = 2 atau x = –1
Harga nol penyebut: tidak ada, karena penyebut tidak dapat difaktorkan dan jika dihitung nilai diskriminannya:
D = b2 – 4.a.c = 12 – 4.1.1 = 1 – 4 = –3
Nilai D-nya negatif, sehingga persamaan tersebut tidak mempunyai akar real
(Catatan: jika nilai D-nya tidak negatif, gunakan rumus abc untuk mendapat harga nol-nya)
Garis bilangan:

Jadi penyelesaiannya: {x | x ≤ –1 atau x ≥ 2}
Pertidaksamaan Irasional/Pertidaksamaan Bentuk Akar
→ variabelnya berada dalam tanda akarPenyelesaian:
- Kuadratkan kedua ruas
- Jadikan ruas kanan sama dengan nol
- Selesaikan seperti menyelesaikan pertidaksamaan linear/kuadrat
- Syarat tambahan: yang berada di dalam setiap tanda akar harus ≥ 0

Kuadratkan kedua ruas:
x2 – 5x – 6 < x2 – 3x + 2
x2 – 5x – 6 – x2 + 3x – 2 < 0
–2x – 8 < 0
Semua dikali –1:
2x + 8 > 0
2x > –8
x > –4
Syarat 1:
x2 – 5x – 6 ≥ 0
(x – 6).(x + 1) ≥ 0
Harga nol: x – 6 = 0 atau x + 1 = 0
x = 6 atau x = –1
Syarat 2:
x2 – 3x + 2 ≥ 0
(x – 2).(x – 1) ≥ 0
Harga nol: x – 2 = 0 atau x – 1 = 0
x = 2 atau x = 1
Garis bilangan:
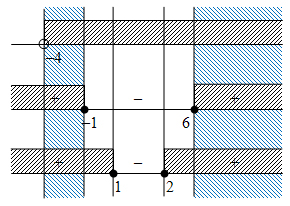
Jadi penyelesaiannya: {x | –4 < x ≤ –1 atau x ≥ 6}
Contoh 2:
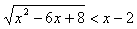
Kuadratkan kedua ruas:
x2 – 6x + 8 < x2 – 4x + 4
x2 – 6x + 8 – x2 + 4x – 4 < 0
–2x + 4 < 0
–2x < –4
Semua dikalikan –1
2x > 4
x > 2
Syarat:
x2 – 6x + 8 ≥ 0
(x – 4).(x – 2) ≥ 0
Harga nol: x – 4 = 0 atau x – 2 = 0
x = 4 atau x = 2
Garis bilangan:

Jadi penyelesaiannya: {x | x ≥ 4}
Pertidaksamaan Nilai Mutlak
→ variabelnya berada di dalam tanda mutlak | ….. |(tanda mutlak selalu menghasilkan hasil yang positif, contoh: |3| = 3; |–3| = 3)
Pengertian nilai mutlak:
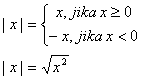
Penyelesaian:
Jika |x| < a berarti: –a < x < a, dimana a ≥ 0
Jika |x| > a berarti: x < –a atau x > a, dimana a ≥ 0
Contoh 1:
|2x – 3| ≤ 5
berarti:
–5 ≤ 2x – 3 ≤ 5
–5 + 3 ≤ 2x ≤ 5 + 3
–2 ≤ 2x ≤ 8
Semua dibagi 2:
–1 ≤ x ≤ 4
Contoh 2:
|3x + 7| > 2
berarti:
3x + 7 < –2 atau 3x + 7 > 2
3x < –2 – 7 atau 3x > 2 – 7
x < –3 atau x > –5/3
Contoh 3:
|2x – 5| < |x + 4|
Kedua ruas dikuadratkan:
(2x – 5)2 < (x + 4)2
(2x – 5)2 – (x + 4)2 < 0
(2x – 5 + x + 4).(2x – 5 – x – 4) < 0 (Ingat! a2 – b2 = (a + b).(a – b))
(3x – 1).(x – 9) < 0
Harga nol: 3x – 1 = 0 atau x – 9 = 0
x = 1/3 atau x = 9
Garis bilangan:

Jadi penyelesaiannya: {x | 1/3 < x < 4}
Contoh 4:
|4x – 3| ≥ x + 1
Kedua ruas dikuadratkan:
(4x – 3)2 ≥ (x + 1)2
(4x – 3)2 – (x + 1)2 ≥ 0
(4x – 3 + x + 1).(4x – 3 – x – 1) ≥ 0
(5x – 2).(3x – 4) ≥ 0
Harga nol: 5x – 2 = 0 atau 3x – 4 = 0
x = 2/5 atau x = 4/3
Syarat:
x + 1 ≥ 0
x ≥ –1
Garis bilangan:

Jadi penyelesaiannya: {x | –1 ≤ x ≤ 2/5 atau x ≥ 4/3}
Contoh 5:
|x – 2|2 – |x – 2| < 2
Misalkan |x – 2| = y
y2 – y < 2
y2 – y – 2 < 0
(y – 2).(y + 1) < 0
Harga nol: y – 2 = 0 atau y + 1 = 0
y = 2 atau y = –1
Garis bilangan:

Artinya:
–1 < y < 2
–1 < |x – 2| < 2
Karena nilai mutlak pasti bernilai positif, maka batas kiri tidak berlaku
|x – 2| < 2
Sehingga:
–2 < x – 2 < 2
–2 + 2 < x < 2 + 2
0 < x < 4


nice blog :) keep posting yah... this really helpful!
yeah this blog is so good! Thank you for posting about it! It's Helpful! :D
sangat membantu sekaLi..
terimakasih banyak :)
trimakasih gan..!! i like that (y)
Mantap, mas. Bisa di jadikan bahan referensi. terimakasih ya
mantapp mas..,ma kasihh banyakkkk :D
Trima kasih ini sangat membantu σ(^○^)
SANGAT AMAT MEMBANTU... terimakasih buat penulis blog ini.. sangat mudah dipahami ... dengan contoh2 soal dan pembahasan nya... top markotop
Bermanfaat
terimakasiiiiiiiiih
Terimakasihh... ini sangat membantu saya :)
terimakasih banyak
thank very much :)
Untuk contoh soal pertidaksamaan harga mutlak no4 sepertinya kurang tepat..karena nilai X+1 belum diketahui nilainya..tidak bisa semena2 dikuadratkan..berbeda dengan soal no3 yg kedua ruas terdapat tanda mutlak dan sudah jelas bernilai positif..soal no 4 lbih tepat dikerjakan dgn cara sifat yg sudah ada..
betul, pertidaksamaan no 4 bagian mutlak salah jawabannya, coba anda masukan
x = - 10, pasti benar.
bentuk soal ini tidak boleh dikuadratkan, penggunaan kuadrat kedua ruas hanya kalau kedua ruas pasti positif.
sangat membantu! terimakasih yaaa
Terima kasih, kami bisa mendapatkan ilmunya. Jawaban no.4 sudah betul, memang perlu syarat, bukankah nilai mutlak selalu bernilai positif atau sama dengan nol. Untuk Mas. Arcadius dan Michael, perlu pelajari dan belajar lagi ya Mas, Ok.
@nur memang nilai mutlak selalu bernilai positif, berarti semua yang di ruas kiri itu positif, tetapi yang di kiri nya itu belum tentu positif bang, x nya sendiri masih bisa saja negatif, jadi belum boleh dikuadrat, harus dibagi 2 kemungkinan dlu, + >= + atau + >= -, lalu dicari penyelesaiannya dari kedua kemungkinan tersebut.
Jadi lebih paham... Terimakasih untuk penjelasannya yang jelas :)
terima kasih :D
bagaimana untuk soal pertidaksamaan dengan pangkat 3
misal nya
xpangkat 3 - 3x + 2 < 0
atau soal berikut
x pangkat 2 >= 5
mohon bantuannya
Terima kasih penjelasannya sangat membantu :)
nice blog!:D keep improve the blog
apa yang dimaksud "mengubah bentuk menjadi tanpa nilai mutlak" ???
thank you
thanks
thanks jelas banget
terima kasih, ini sangat membantu
sangat membantu
wow, terima kasih sangat membantu
Gua ulangan dapet nilai bagus vro,membntu bnget lahh
Blog anda sangat bermanfaat,Tuhan memberkati��
Nice postingannya bro....... Besok mau ulangan nih,,, membantu banget "thanks"
thanks gan
Maacihhh banget blognya.membantu banget buat ngerjain tugas saya..
wow
sngat mmbntu gua bgt nic
thank bro
OBRIGADO
jika soal dari pertidaksamaan pecahan mempunyai pembilang pertidak samaan kuadrat, dan bagian penyebutnya adalah linea, bagaimana cara penyelesaiannya?
mohon penjelasannya!
Thanks gan, bermanfaat banget nih..
terimakasih bro.... siiippppp
Terima kasih banyaakk insyaAllah sangaf membantu
Mohon doanya ya semua semoga saya bisa lolos kedokteran 2015/2016!:😀
Aamiin Allahumma Aamiin
Terimakasih🙏
gimana kalau
-2<=|x-2|<=3 ?
Terimakasih, sangat membantu :)
Gimana klw soalnya | 2x + 3 | + 2 | 3x + 2 |^ > 6
ketemu deh, belajar dulu lah tuk uts besok, hehe terimakasih
beBisnis lah
bro aturan pertidaksamaan ada gk? ane nemunya sifat2nya mlulu
terimakasih.semoga ilmunya bermanfaat untuk penulis dan pembaca.
lebih teliti lagi buat yag punya blog,
banyak yg harus dikoreksi cara pengerjaan soalnya
izin copas gan, buat tugas
izin copas gan, buat tugas
sankyu
it helps me so much.
keep sharing yeahhh...
Jika │x + 2│=3│x-4│,bagaimana caranya?
Bagaimana penyelesaian dari x+1 > x-6 ?
min link ada terlalu sering di copas orang lain ini salah satunya
https://windakomala96.blogspot.co.id/2014/10/tips-membuat-games-tanpa-berbasis-coding.html?showComment=1473294939466#c8836722095778071470
. Tentukan himpunan jawab pertidaksamaan
i. │x2 – x│≤2
ii. │x2 – x – 1│≤1
Terimakasih
Semoga lebih bagus lagi 👍
nice blog :)
Makasih ^^
Mantap!
Saya sedang butuh materi ini.
Karena masih susah memahami garis bilangannya.
Sangat bermanfaat.. Thanks
Lengkap banget,makasih ya
Alhamdulillah jadi ngerti makasii
Nice post!
Manatap slurr