|
Turunan fungsi f ‘ (x) didefinisikan sebagai :

Rumus-rumus Turunan :
untuk a = konstanta
jika U = u(x) dan V = v(x) adalah suatu fungsi
Jangan sampai lupa yah, setiap fungsi yang hendak diturunkan, pastikan dinyatakan dalam bentuk perpangkatan terlebih dulu, let’s cekidot …
Contoh dan pembahasan turunan fungsi:
Tentukan turunan pertama dari :
Soal2
1. Fungsi f ditentukan oleh dan f ‘ adalah turunan pertama dari f. Maka nilai dari f ‘(1) = ….
dan f ‘ adalah turunan pertama dari f. Maka nilai dari f ‘(1) = ….

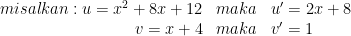
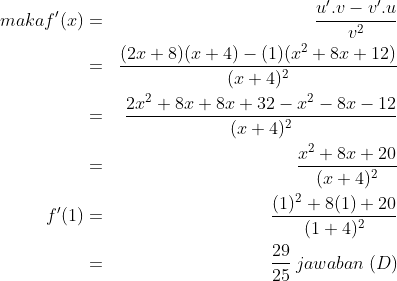 $
$
2. Turunan pertama fungsi adalah f ‘(x) = ….
adalah f ‘(x) = ….


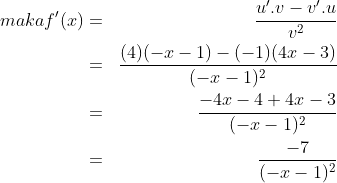 3. Diketahui
3. Diketahui  dan f ‘(x) adalah turunan pertama dari f(x). Maka nilai dari f ‘(-1) = ….
dan f ‘(x) adalah turunan pertama dari f(x). Maka nilai dari f ‘(-1) = ….

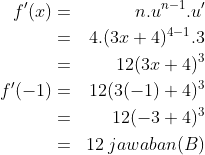
4. Turunan pertama fungsi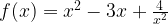 adalah f ‘(x) = ….
adalah f ‘(x) = ….
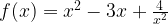 nyatakan dalam bentuk pangkat
nyatakan dalam bentuk pangkat
 5. Turunan pertama dari
5. Turunan pertama dari 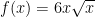 adalah f ‘(x) = …
adalah f ‘(x) = …
 nyatakan dalam bentuk pangkat
nyatakan dalam bentuk pangkat
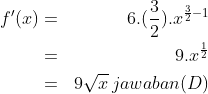
Rumus-rumus Turunan :
untuk a = konstanta
maka
maka
maka
jika U = u(x) dan V = v(x) adalah suatu fungsi
maka
maka
maka
maka
maka
dinamakan aturan rantai
Jangan sampai lupa yah, setiap fungsi yang hendak diturunkan, pastikan dinyatakan dalam bentuk perpangkatan terlebih dulu, let’s cekidot …
Contoh dan pembahasan turunan fungsi:
Tentukan turunan pertama dari :
-
Jawab :
-
Jawab :* nyatakan dalam bentuk pangkat terlebih dulu menjadi* maka : -
Jawab :* nyatakan dalam bentuk pangkat terlebih dulu menjadi* maka : -
Jawab :* kita misalkan* maka : -
Jawab :* kita misalkandan
* lalu kita pakai( aturan rantai )
Soal2
1. Fungsi f ditentukan oleh
a. 
b. 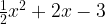
c. 
d. 
e. 
jawab:2. Turunan pertama fungsi
a. 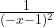
b. 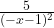
c. 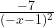
d. 
e. 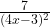
jawab:a. 4
b. 12
c. 16
d. 84
e. 112
jawab:misalkan u = 3x + 4 maka u’ = 3 dan n = 4
gunakan aturan rantai, maka :
4. Turunan pertama fungsi
a. 
b. 
c. 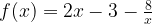
d. 
e. 
jawab:a.
b. 
c. 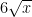
d. 
e. 
jawab:maka :
- Jika
maka g ‘(2) = …. A. -30
B. -10
C. 30
D. 60
E. 90
Jawab :
* misalmaka
* kita pakai aturan rantai sehingga :
- Jika
maka f ‘(x) = … A.
B.
C.
D.
E.
Jawab :
* terdapat dua suku yang harus diturunkan, kita turunkan suku yang pertama secara langsung dan suku yang kedua menggunakan rumus* perhatikan suku kedua misalkan :
maka
- Turunan pertama dari
adalah ….. A.
B.
C.
D.
E.
Jawab :
* untuk model soal yang seperti ini kita kalikan pembilangnya sehingga menjadi bentuk kuadrat, didapatbaru kita gunakan
* misalkan* maka :
- Diketahui
maka
= …. A.
B.
C.
D.
E.
Jawab :
* nyatakan y dalam bentuk pangkat menjadi* nah…ingat kita pakai aturan rantai
- Jika
maka f ‘ (1) = … A. -4
B. -2
C. -1
D. 0
E.
Jawab :
* masih ingatkah materi komposisi fungsi ….???* kita misalkan
*subitusikan kemenjadi :
* baru kita turunkan tiap sukunya
- Turunan pertama dari f(x) = 7 cos (5 – 3x) adalah f ‘ (x) = ….. A. 35 sin (5 – 3x) B. - 15 sin (5 – 3x) C. 21 sin (5 – 3x) D. - 21 sin (5 – 3x) E. - 35 sin (5 – 3x) Jawab :
- Jika f ‘(x) adalah turunan dari f(x) dan jika f(x) = ( 3x – 2 ) sin (2x + 1) maka f ‘ (x) adalah … A. 3 cos ( 2x + 1 ) B. 6 cos ( 2x + 1 ) C. 3 sin ( 2x + 1 ) + (6x – 4) cos (2x + 1) D. (6x – 4) sin ( 2x + 1 ) + 3 cos ( 2x + 1 ) E. 3 sin ( 2x + 1) + ( 3x – 2 ) cos( 2x + 1 ) Jawab :
- Turunan pertama fungsi f (x) = 5 sin x cos x adalah f ‘ (x) = … A. 5 sin 2x B. 5 cos 2x C. 5 sin2 x cos x D. 5 sin x cos2 x E. 5 sin 2x cos x Jawab :
- Jika
, maka nilai dari f ‘ (0) = …..
A . - Turunan pertama dari
adalah f ’ (x) =……
A. -
* ingat 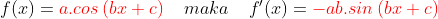
* maka:
* 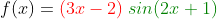 kita misalkan terlebih dulu
kita misalkan terlebih dulu
* ingat rumus turunan perkalian dua fungsi :
*  kita misalkan terlebih dulu
kita misalkan terlebih dulu
* ingat rumus turunan
eitttts…..tapi cara yang satu ini lebih simple…kita bisa pakai neh,cekidot…
* ingat bahwa 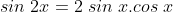
* sehingga :
* maka :
Dengan hasil yang sama namun lebih cepat dalam pengerjaannya…silahkan pilih cara yang lebih disukai…
* perlu diingat bahwa :
* nah, baru kita misalkan 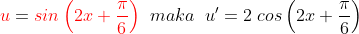
* fungsi menjadi 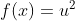 baru pakai aturan rantai
baru pakai aturan rantai 
* pengerjaannya hampir sama dengan soal no.4 kita misalkan terlebih dulu
* didapat 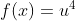 kita pakai aturan rantai
kita pakai aturan rantai 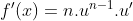 maka :
maka :
ups….saat kita cek di pilgan ternyata jawaban tersebut tidak ada pilihannya, so lanjut ke next step ….
* ingat bahwa 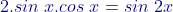
taraaaaa…..selesai sudah latihan soal dan pembahasan turunan trigonometri kita…
semoga bermanfaat yah….
semoga bermanfaat yah….


bermanfaat skli gan thank u
sangat bermanfaat
makasi ^_^
thnk :))
Rumus2 dasar ini sangat membantu dan mmengingatkan kmbali dan menjadi penyegaran bagiku dan terima kasih untuk smuanaya.
terima kasih.. :)
Makasih bgt bro info nya, sangat bermanfaat buat saya. hehe
Jangan Lupa mampir ke blog Lowongan Kerja Terbaru ane ya Lowongan BANK
soal 2 no 1 salah deh sepertinya, coba cek kebali, bagian perkalian U' x V
kamu copy paste yak? ada yg salah tuh!
Walaupun ada yang salah tp kalo bwt saya, dengan membaca sekilas udah ngerti koq hehehe. THANKS YA GAN.... MEMBANTU SAAT GW UAS....
nih sebagai imbalan ya gan... kalo mau refreshing untuk nonton film atau main game download aja ya... di www.albertus-cp.blogspot.com
thank gans
Terimakasih